NATURE

27 November 2003

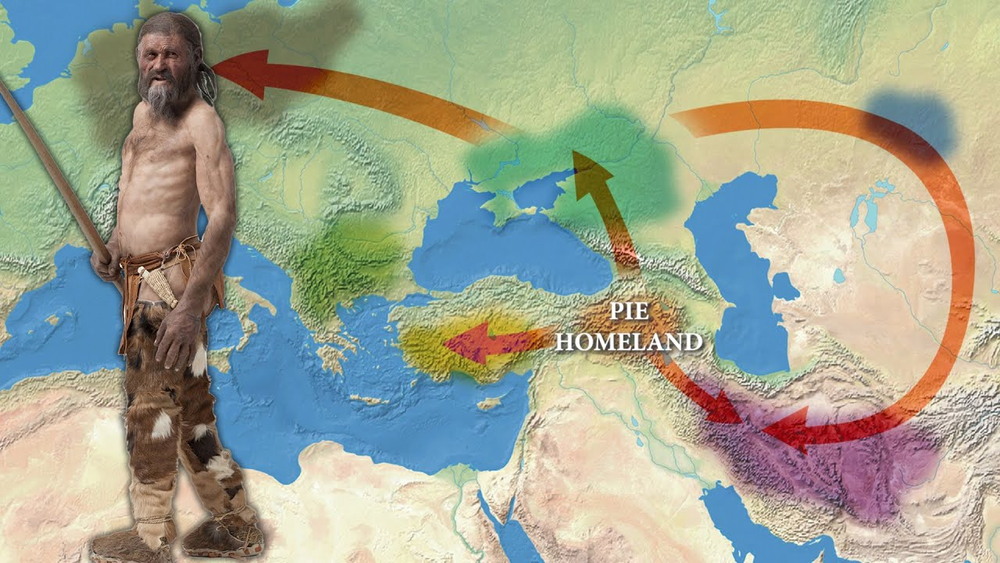
NEW DNA ANALYSIS SHED LIGHT TO INDO-EUROPEAN HOMELAND
Humanity first spread from Zagros to Europe and South Asia

Could this all be a coincidence?
-- There is a Britan (Beritan/Bêrtî) Kurdish tribe (Serhed)
-- There is a German (Germian) Kurdish tribe (Kerkuk, Kelar)
-- Goti (Goyi) kurd tribe (Hekari)
-- There is the Swedî (Svedki) Kurdish tribe (Çolig, Bingol)

-- We do not know by now if there is a name and place in Kurdistan which is connected with the Ions (Greeks), but if it is researched, it definitely exists.

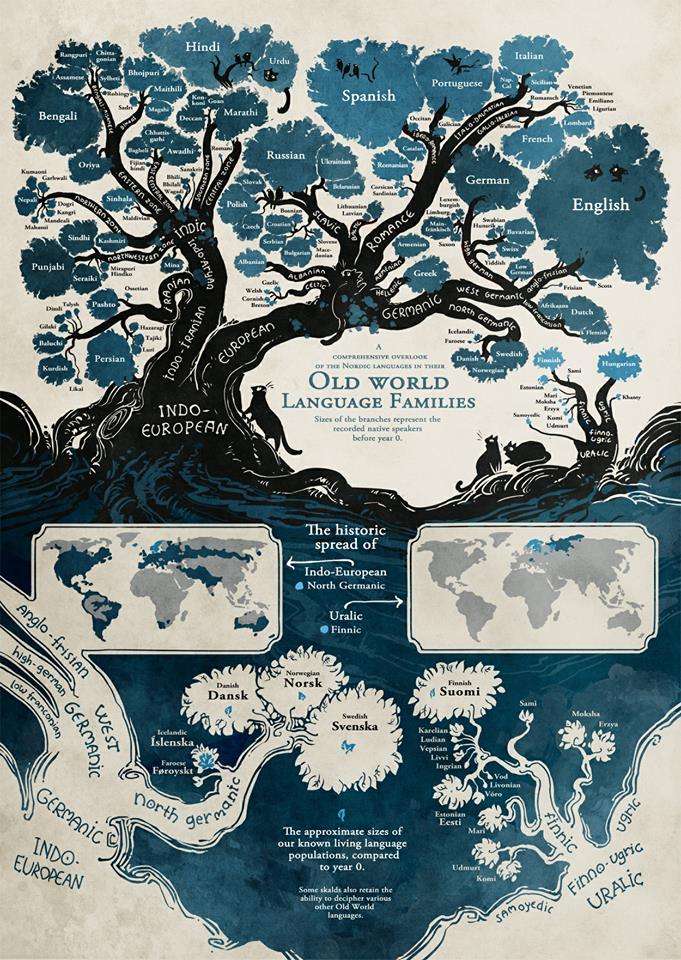
In the Research on the Origin of Indo-European Languages, initiated by the University of Auckland in New Zealand in 1980 and partially published in the prestigious journal Nature in the autumn of 2003, "the origin of all Indo-European languages" was found in the Neolithic Period of Kurdistan. It was claimed to be the revir basin of the Tigris and Eufrat rivers.

Probably this is not just a coincidence.

When the origins of Hindu-European languages ??and tribes were investigated at Auckland University, there was no Kurdish-speaking etymologist in this study group. Today's Kurdish etymologists quite rightly find the work of this group very incomplete. Because when the information about Kurdish, which is a very old Indo-European language, is considered in this group, only the missing information about the Kurdish language given by 17th and 18th century European archaeologists, travelers and orientalists has been evaluated. It has been revealed today that the approaches of these archaeologists and travelers regarding the Kurds and the Kurdish language are centered on racism and Christian chauvinism.

Now there are Kurdish etymologists who speak Greek and also speak very good ancient Greek, and they reveal that the ancient Greek language shows great similarities with the Kurdish language, which is a much older language than Greek. One of these Kurdish etymologists is Ali Karduxos.

Do you think this is just a coincidence?

Prehistoric Farmer of Eastern Anatolia (Kurdistan)

"The Kurds are the grandchildren of the first shepherds who have been in the mountains of Kurdistan since the Stone Age."

Geneticists David Comas

Nature 426, 435 - 439 (27 November 2003); doi:10.1038/nature02029

Language-tree divergence times support the Anatolian theory of Indo-European origin
RUSSELL D. GRAY AND QUENTIN D. ATKINSON

Department of Psychology, University of Auckland, Private Bag 92019, Auckland 1020, New Zealand

Correspondence and requests for materials should be addressed to R.G. (rd.gray@auckland.ac.nz).
Languages, like genes, provide vital clues about human history1, 2. The origin of the Indo-European language family is "the most intensively studied, yet still most recalcitrant, problem of historical linguistics"3. Numerous genetic studies of Indo-European origins have also produced inconclusive results4-6. Here we analyse linguistic data using computational methods derived from evolutionary biology. 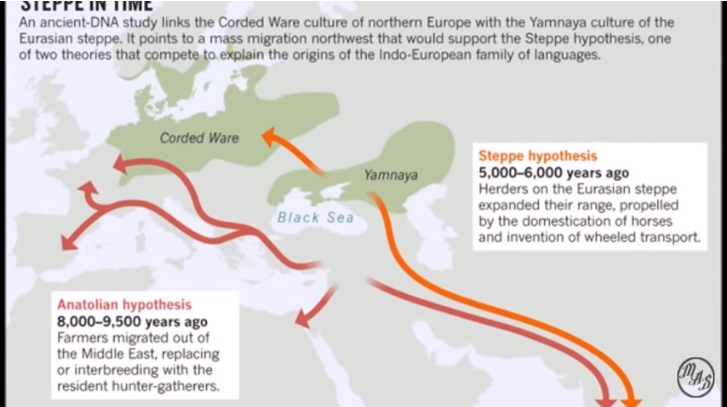We test two theories of Indo-European origin: the 'Kurgan expansion' and the 'Anatolian farming' hypotheses. The Kurgan theory centres on possible archaeological evidence for an expansion into Europe and the Near East by Kurgan horsemen beginning in the sixth millennium BP7, 8. In contrast, the Anatolian theory claims that Indo-European languages expanded with the spread of agriculture from Anatolia around 8,000–9,500 years BP9. In striking agreement with the Anatolian hypothesis, our analysis of a matrix of 87 languages with 2,449 lexical items produced an estimated age range for the initial Indo-European divergence of between 7,800 and 9,800 years BP. These results were robust to changes in coding procedures, calibration points, rooting of the trees and priors in the bayesian analysis.

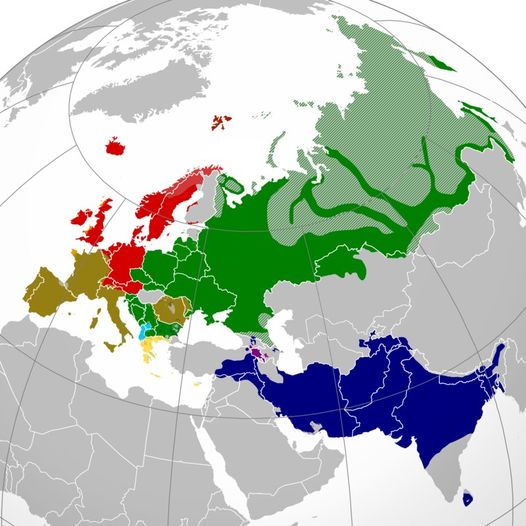
Map of Indo-European Geography

Historical linguists traditionally use the 'comparative method' to construct language family trees from discrete lexical, morphological and phonological data. Unfortunately, although the comparative method can provide a relative chronology, it cannot provide absolute date estimates. An alternative method of analysis is glottochronology. This derivative of lexicostatistics is a distance-based approach to language-tree construction that enables absolute dates to be estimated10. Glottochronology uses the percentage of shared 'cognates' between languages to calculate divergence times by assuming a constant rate of lexical replacement or 'glottoclock'. Cognates are words inferred to have a common historical origin because of systematic sound correspondences and clear similarities in form and meaning. Despite some initial enthusiasm, the method has been heavily criticized and is now largely discredited11, 12. Criticisms of glottochronology, and distance-based methods in general, tend to fall into four main categories: first, by summarizing cognate data into percentage scores, much of the information in the discrete character data is lost, greatly reducing the power of the method to reconstruct evolutionary history accurately13; second, the clustering methods used tend to produce inaccurate trees when lineages evolve at different rates, grouping together languages that evolve slowly rather than languages that share a recent common ancestor12, 14; third, substantial borrowing of lexical items between languages makes tree-based methods inappropriate; and fourth, the assumption of a strict glottoclock rarely holds, making date estimates unreliable11. For these reasons, historical linguists have generally abandoned efforts to estimate absolute ages. Dixon15 epitomizes this view with his assertion that, on the basis of linguistic data, the age of Indo-European "could be anything—4,000 years BP or 40,000 years BP are both perfectly possible (as is any date in between)".

Recent advances in computational phylogenetic methods, however, provide possible solutions to the four main problems faced by glottochronology. First, the problem of information loss that comes from converting discrete characters into distances can be overcome by analysing the discrete characters themselves to find the optimal tree(s). Second, the accuracy of tree topology and branch-length estimation can be improved by using models of evolution. Maximum-likelihood methods generally outperform distance and parsimony approaches in situations where there are unequal rates of change14. Moreover, uncertainty in the estimation of tree topology, branch lengths and parameters of the evolutionary model can be estimated using bayesian Markov chain Monte Carlo16 (MCMC) methods in which the frequency distribution of the sample approximates the posterior probability distribution of the trees17. All subsequent analyses can then incorporate this uncertainty. Third, lexical items that are obvious borrowings can be removed from the analysis, and computational methods such as split decomposition18, which do not force the data to fit a tree model, can be used to check for non-tree-like signals in the data. Finally, the assumption of a strict clock can be relaxed by using rate-smoothing algorithms to model rate variation across the tree. The penalized-likelihood19 model allows rate variation between lineages while incorporating a 'roughness penalty' that penalizes changes in rate from branch to branch. This smoothes inferred rate variation across the tree so that the age of any node can be estimated even under conditions of rate heterogeneity.

We applied likelihood models of lexical evolution, bayesian inference of phylogeny and rate-smoothing algorithms to a matrix of 87 Indo-European languages with 2,449 cognate sets coded as discrete binary characters. This coding was based on the Indo-European database of Dyen et al.20, with the addition of three extinct languages. Examining subsets of languages using split decomposition revealed a strong tree-like signal in the data, and a preliminary parsimony analysis produced a consistency index of 0.48 and a retention index of 0.76, well above what would be expected from biological data sets of a similar size21. The consensus tree from an initial analysis is shown in Fig. 1a. The topology of the tree is consistent with the traditional Indo-European language groups22. All of these groups are monophyletic and supported by high posterior probability values. Recent parsimony and compatibility analyses have also supported these groupings, as well as a Romano-Germano-Celtic supergroup, the early divergence of Greek and Armenian lineages23, and the basal position of Tocharian24. The consensus tree also reflects traditional uncertainties in the relationships between the major Indo-European language groups. For instance, historical linguists have not resolved the position of the Albanian group and our results clearly reflect this uncertainty (the posterior probability of the Albanian/Indo-Iranian group is only 0.36).

Figure 1 Consensus tree and divergence-time estimates. Full legend

High resolution image and legend (154k)One important advantage of the bayesian MCMC approach is that any inferences are not contingent on a specific tree topology. Trees are sampled in proportion to their posterior probability, providing a direct measure of uncertainty in the tree topology and branch-length estimates. By estimating divergence times across the MCMC sample distribution of trees, we can explicitly account for variability in the age estimates due to phylogenetic uncertainty, and hence calculate a confidence interval for the age of any node. We estimated divergence times by constraining the age of 14 nodes on each tree in accordance with historically attested events (see Supplementary Information). We then used penalized-likelihood rate smoothing to calculate divergence times without the assumption of rate constancy19. Another advantage of the bayesian framework is that prior knowledge of language relationships can be incorporated into the analysis. To ensure that the sample was consistent with well-established linguistic relationships, we filtered the 10,000-tree sample using a constraint tree (Fig. 1b). We used the resulting distribution of 3,500 estimates of basal divergence times to create a confidence interval for the age of the Indo-European language family (Fig. 1b).

A key part of any bayesian phylogenetic analysis is an assessment of the robustness of the inferences. One important potential cause of error is cognacy judgements. In the initial analysis, we included all cognate sets in the Dyen et al. database20 in an effort to maximize phylogenetic signal. To assess the impact of different levels of stringency in the cognacy judgements, we repeated the analysis after removing all cognate sets identified by Dyen et al. as 'doubtful'. 'Doubtful cognates' (for instance, possible chance similarities) could falsely increase similarities between languages and thus lead to an underestimate of the divergence times. Unrecognized borrowing between closely related languages would have a similar effect. Conversely, borrowing between distantly related languages will falsely inflate branch lengths at the base of the tree and thus increase divergence-time estimates. With the doubtful cognates removed, the conservative coding led to a similar estimate of Indo-European language relationships to that produced using the original coding. The relationships within each of the 11 main groups were unchanged. Only the placement of the weakly supported basal branches differed (Fig. 1c). More significantly, the divergence-time estimates increased, suggesting that the effects of chance similarities and unrecognized borrowings between closely related languages might have outweighed those of borrowings between distantly related languages. In other words, our initial analysis is likely to have underestimated the age of Indo-European.

The constraint tree used to filter the MCMC sample of trees also contained assumptions about Indo-European history that might have biased the results. We therefore repeated the analyses using a more relaxed set of constraints (Fig. 1d). This produced a divergence-time distribution and consensus tree almost identical to the original sample distribution (Fig. 1d).

Another potential bias lay in the initial coding procedure, which made no allowance for missing cognate information. The languages at the base of the tree (Hittite, Tocharian A and Tocharian B) may appear to lack cognates found in other languages because our knowledge of these extinct languages is limited to reconstructions from ancient texts. This uneven sampling might have increased basal branch lengths and thus inflated estimates of divergence times. We tested this possibility by recoding apparently absent cognates as uncertainties (absent or present) and re-running the analyses. Although divergence-time estimates decreased slightly, the effect was only small (Fig. 1e).

Finally, although there is considerable support for Hittite (an extinct Anatolian language) as the most appropriate root for Indo-European22, 23, rooting the tree with Hittite could be claimed to bias the analysis in favour of the Anatolian hypothesis. We thus re-ran the analysis using the consensus tree in Fig. 1 rooted with Balto-Slavic, Greek and Indo-Iranian as outgroups. This increased the estimated divergence time from 8,700 years BP to 9,600, 9,400 and 10,100 years BP, respectively.

The pattern and timing of expansion suggested by the four analyses in Fig. 1 is consistent with the Anatolian farming theory of Indo-European origin. Radiocarbon analysis of the earliest Neolithic sites across Europe suggests that agriculture arrived in Greece at some time during the ninth millennium BP and had reached as far as Scotland by 5,500 years BP25. Figure 1 shows the Hittite lineage diverging from Proto-Indo-European around 8,700 years BP, perhaps reflecting the initial migration out of Anatolia. Tocharian, and the Greco-Armenian lineages are shown as distinct by 7,000 years BP, with all other major groups formed by 5,000 years BP. This scenario is consistent with recent genetic studies supporting a Neolithic, Near Eastern contribution to the European gene pool4, 6. The consensus tree also shows evidence of a period of rapid divergence giving rise to the Italic, Celtic, Balto-Slavic and perhaps Indo-Iranian families that is intriguingly close to the time suggested for a possible Kurgan expansion. Thus, as observed by Cavalli-Sforza et al.26, these hypotheses need not be mutually exclusive.

Phylogenetic methods have revolutionized evolutionary biology over the past 20 years and are now starting to take hold in other areas of historical inference2, 23, 24, 27-29. The model-based bayesian framework used in this paper offers several advantages over previous applications of computational methods to language phylogenies. This approach allowed us to: identify sections in the language tree that were poorly supported; explicitly incorporate this uncertainty in tree typology and branch-length estimates in our analysis; test the possible effects of borrowing, chance similarities and bayesian priors on our analysis; and estimate divergence times without the assumption of a strict glottoclock. The challenge of making accurate inferences about human history is an extremely demanding one, requiring the integration of archaeological, genetic, cultural and linguistic data. The combination of computational phylogenetic methods and lexical data to test archaeological hypotheses is a step forward in this challenging and fascinating task.

Methods
Data and coding Data were sourced from the comparative Indo-European database created by Dyen et al.20. The database records word forms and cognacy judgements in 95 languages across the 200 items in the Swadesh word list. This list consists of items of basic vocabulary such as pronouns, numerals and body parts that are known to be relatively resistant to borrowing. For example, although English is a Germanic language, it has borrowed around 50% of its total lexicon from French and Latin. However, only about 5% of English entries in the Swadesh 200-word list are clear Romance language borrowings1. Where borrowings were obvious, Dyen et al. did not score them as cognate and thus they were excluded from our analysis; 11 of the speech varieties that were not coded by Dyen et al. were also excluded. To facilitate reconstruction of some of the oldest language relationships, we added three extinct Indo-European languages, thought to fit near the base of the tree (Hittite, Tocharian A and Tocharian B). Word form and cognacy judgements for all three languages were made on the basis of multiple sources to ensure reliability. The presence or absence of words from each cognate set was coded as '1' or '0', respectively, to produce a binary matrix of 2,449 cognates in 87 languages.

Tree construction Language trees were constructed using a 'restriction site' model of evolution that allows unequal character-state frequencies and gamma-distributed character-specific rate heterogeneity (MrBayes version 2.01; ref. 30). We used default 'flat' priors for the rate matrix, branch lengths, gamma shape parameter and site-specific rates. The results were found to be robust to changes in these priors. For example, repeating the analyses with an exponential branch-length prior produced a 95% confidence interval for the basal divergence time of between 7,100 and 9,200 years BP.
The program was run ten times using four concurrent Markov chains. Each run generated 1,300,000 trees from a random starting phylogeny. On the basis of an autocorrelation analysis, only every 10,000th tree was sampled to ensure that consecutive samples were independent. A 'burn-in' period of 300,000 trees for each run was used to avoid sampling trees before the run had reached convergence. Log-likelihood plots and an examination of the post-burn-in tree topologies showed that the runs had indeed reached convergence by this time. For each analysis a total of 1,000 trees were sampled and rooted with Hittite. The branch between Hittite and the rest of the tree was split at the root such that half its length was assigned to the Hittite branch and half to the remainder of the tree; divergence-time estimates were found to be robust to threefold alterations of this allocation.

Divergence-time estimates Eleven nodes corresponding to the points of initial divergence in all of the major language subfamilies were given minimum and/or maximum ages on the basis of known historical information (see Supplementary Information). The ages of all terminal nodes on the tree, representing languages spoken today, were set to zero by default. Hittite and the Tocharic languages were constrained in accordance with estimated ages of the source texts. Relatively broad date ranges were chosen to avoid making disputable, a priori assumptions about Indo-European history. A likelihood ratio test with the extinct languages removed revealed that rates were significantly non-clock-like ( 2 = 787.3, d.f. = 82, P < 0.001). Divergence-time estimates were thus made using the semi-parametric, penalized-likelihood model of rate variation implemented in R8s (version 1.50)19. The cross-validation procedure was applied to the majority-rule consensus tree (Fig. 1) to determine the optimal value of the rate-smoothing parameter. Step-by-step removal of each of the 14 age constraints on the consensus tree revealed that divergence-time estimates were robust to calibration errors. For 13 nodes, the reconstructed age was within 390 years of the original constraint range. Only the reconstructed age for Hittite showed an appreciable variation from the constraint range. This may be attributable to the effect of missing data associated with extinct languages. Reconstructed ages at the base of the tree ranged from 10,400 years BP with the removal of the Hittite age constraint, to 8,500 years BP with the removal of the Iranian group age constraint.
Supplementary information accompanies this paper.

Received 18 July 2003; accepted 22 August 2003

References
1. Pagel, M. in Time Depth in Historical Linguistics (eds Renfrew, C., McMahon, A. & Trask, L.) 189–207 (The McDonald Institute for Archaeological Research, Cambridge, UK, 2000)
2. Gray, R. D. & Jordan, F. M. Language trees support the express-train sequence of Austronesian expansion. Nature 405, 1052–1055 (2000) | Article | PubMed | ISI | ChemPort |3. Diamond, J. & Bellwood, P. Farmers and their languages: the first expansions. Science 300, 597–603 (2003) | Article | PubMed | ISI | ChemPort |4. Richards, M. et al. Tracing European founder lineage in the Near Eastern mtDNA pool. Am. J. Hum. Genet. 67, 1251–1276 (2000) | PubMed | ISI | ChemPort |5. Semoni, O. et al. The genetic legacy of Paleolithic Homo sapiens in extant Europeans: a Y chromosome perspective. Science 290, 1155–1159 (2000) | Article | PubMed | ISI | ChemPort |6. Chikhi, L., Nichols, R. A., Barbujani, G. & Beaumont, M. A. Y genetic data support the Neolithic Demic Diffusion Model. Proc. Natl Acad. Sci. USA 99, 11008–11013 (2002) | Article | PubMed | ChemPort |7. Gimbutas, M. The beginning of the Bronze Age in Europe and the Indo-Europeans 3500–2500 B.C. J. Indo-Eur. Stud. 1, 163–214 (1973)
8. Mallory, J. P. Search of the Indo-Europeans: Languages, Archaeology and Myth (Thames & Hudson, London, 1989)
9. Renfrew, C. in Time Depth in Historical Linguistics (eds Renfrew, C., McMahon, A. & Trask, L.) 413–439 (The McDonald Institute for Archaeological Research, Cambridge, UK, 2000)
10. Swadesh, M. Lexico-statistic dating of prehistoric ethnic contacts. Proc. Am. Phil. Soc. 96, 453–463 (1952)
11. Bergsland, K. & Vogt, H. On the validity of glottochronology. Curr. Anthropol. 3, 115–153 (1962) | Article | ISI |12. Blust, R. in Time Depth in Historical Linguistics (eds Renfrew, C., McMahon, A. & Trask, L.) 311–332 (The McDonald Institute for Archaeological Research, Cambridge, UK, 2000)
13. Steel, M. A., Hendy, M. D. & Penny, D. Loss of information in genetic distances. Nature 333, 494–495 (1988) | Article | PubMed |14. Swofford, D. L., Olsen, G. J., Waddell, P. J. & Hillis, D. M. in Molecular Systematics (eds Hillis, D., Moritz, C. & Mable, B. K.) 407–514 (Sinauer Associates, Inc, Sunderland, Massachusetts, 1996)
15. Dixon, R. M. W. The Rise and Fall of Language (Cambridge Univ. Press, Cambridge, UK, 1997)
16. Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. Equations of state calculations by fast computing machines. J. Chem. Phys. 21, 1087–1091 (1953) | ISI | ChemPort |17. Huelsenbeck, J. P., Ronquist, F., Nielsen, R. & Bollback, J. P. Bayesian inference of phylogeny and its impact on evolutionary biology. Science 294, 2310–2314 (2001) | Article | PubMed | ISI | ChemPort |18. Huson, D. H. SplitsTree: analyzing and visualizing evolutionary data. Bioinformatics 14, 68–73 (1998) | Article | PubMed | ISI | ChemPort |19. Sanderson, M. R8s, Analysis of Rates of Evolution,Version 1.50 (Univ. California, Davis, 2002)
20. Dyen, I., Kruskal, J. B. & Black, P. FILE IE-DATA1. Available at http://www.ntu.edu.au/education/langs/ielex/IE-DATA1 (1997).21. Sanderson, M. J. & Donoghue, M. J. Patterns of variation in levels of homoplasy. Evolution 43, 1781–1795 (1989) | ISI |22. Gamkrelidze, T. V. & Ivanov, V. V. Trends in Linguistics 80: Indo-European and the Indo-Europeans (Mouton de Gruyter, Berlin, 1995)
23. Rexova, K., Frynta, D. & Zrzavy, J. Cladistic analysis of languages: Indo-European classification based on lexicostatistical data. Cladistics 19, 120–127 (2003) | Article | ISI |24. Ringe, D., Warnow, T. & Taylor, A. IndoEuropean and computational cladistics. Trans. Philol. Soc. 100, 59–129 (2002) | Article | ISI |25. Gkiasta, M., Russell, T., Shennan, S. & Steele, J. Neolithic transition in Europe: the radiocarbon record revisited. Antiquity 77, 45–62 (2003) | ISI |26. Cavalli-Sforza, L. L., Menozzi, P. & Piazza, A. The History and Geography of Human Genes (Princeton Univ. Press, Princeton, 1994)
27. Holden, C. J. Bantu language trees reflect the spread of farming across sub-Saharan Africa: a maximum-parsimony analysis. Proc. R. Soc. Lond. B 269, 793–799 (2002) | Article | PubMed | ISI |28. Barbrook, A. C., Howe, C. J., Blake, N. & Robinson, P. The phylogeny of The Canterbury Tales. Nature 394, 839 (1998) | Article | ISI | ChemPort |29. McMahon, A. & McMahon, R. Finding families: Quantitative methods in language classification. Trans. Philol. Soc. 101, 7–55 (2003) | Article | ISI |30. Huelsenbeck, J. P. & Ronquist, F. MRBAYES: Bayesian inference of phylogeny. Bioinformatics 17, 754–755 (2001) | Article | PubMed | ISI | ChemPort |Acknowledgements. We thank S. Allan, L. Campbell, L. Chikhi, M. Corballis, N. Gavey, S. Greenhill, J. Hamm, J. Huelsenbeck, G. Nichols, A. Rodrigo, F. Ronquist, M. Sanderson and S. Shennan for useful advice and/or comments on the manuscript.
Competing interests statement. The authors declare that they have no competing financial interests.

________________________________________
© 2003 Nature Publishing Group

* * *

Language-tree divergence times support the Anatolian theory of
Indo-European origin

Russell D. Gray and Quentin D. Atkinson

Department of Psychology, University of Auckland, Private Bag 92019, Auckland 1020, New Zealand

Correspondence to: Russell D. Gray Email: rd.gray@auckland.ac.nz

Languages, like genes, provide vital clues about human history1, 2. The origin of the Indo-European language family is "the most intensively studied, yet still most recalcitrant, problem of historical linguistics"3. Numerous genetic studies of Indo-European origins have also produced inconclusive results4, 5, 6. Here we analyse linguistic data using computational methods derived from evolutionary biology. We test two theories of Indo-European origin: the 'Kurgan expansion' and the 'Anatolian farming' hypotheses. The Kurgan theory centres on possible archaeological evidence for an expansion into Europe and the Near East by Kurgan horsemen beginning in the sixth millennium BP7, 8. In contrast, the Anatolian theory claims that Indo-European languages expanded with the spread of agriculture from Anatolia around 8,000–9,500 years bp9. In striking agreement with the Anatolian hypothesis, our analysis of a matrix of 87 languages with 2,449 lexical items produced an estimated age range for the initial Indo-European divergence of between 7,800 and 9,800 years bp. These results were robust to changes in coding procedures, calibration points, rooting of the trees and priors in the bayesian analysis.

Recent advances in computational phylogenetic methods, however, provide possible solutions to the four main problems faced by glottochronology. First, the problem of information loss that comes from converting discrete characters into distances can be overcome by analysing the discrete characters themselves to find the optimal tree(s). Second, the accuracy of tree topology and branch-length estimation can be improved by using models of evolution. Maximum-likelihood methods generally outperform distance and parsimony approaches in situations where there are unequal rates of change14. Moreover, uncertainty in the estimation of tree topology, branch lengths and parameters of the evolutionary model can be estimated using bayesian Markov chain Monte Carlo16 (MCMC) methods in which the frequency distribution of the sample approximates the posterior probability distribution of the trees17. All subsequent analyses can then incorporate this uncertainty. Third, lexical items that are obvious borrowings can be removed from the analysis, and computational methods such as split decomposition18, which do not force the data to fit a tree model, can be used to check for non-tree-like signals in the data. Finally, the assumption of a strict clock can be relaxed by using rate-smoothing algorithms to model rate variation across the tree. The penalized-likelihood19 model allows rate variation between lineages while incorporating a 'roughness penalty' that penalizes changes in rate from branch to branch. This smoothes inferred rate variation across the tree so that the age of any node can be estimated even under conditions of rate heterogeneity.

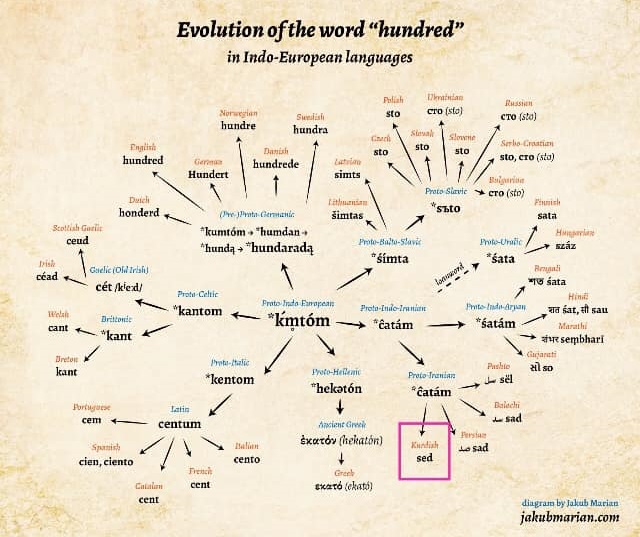
The evolution of the world "hundred" in Indonesia European languages

Kurdish - sed
Russian - ??? (sto)
?Persian - sad
?English - hundred
?German - hundert

a, Majority-rule consensus tree based on the MCMC sample of 1,000 trees. The main language groupings are colour coded. Branch lengths are proportional to the inferred maximum-likelihood estimates of evolutionary change per cognate. Values above each branch (in black) express the bayesian posterior probabilities as a percentage. Values in red show the inferred ages of nodes in years BP. *Italic also includes the French/Iberian subgroup. Panels b–e show the distribution of divergence-time estimates at the root of the Indo-European phylogeny for: b, initial assumption set using all cognate information and most stringent constraints (Anatolian, Tocharian, (Greek, Armenian, Albanian, (Iranian, Indic), (Slavic, Baltic), ((North Germanic, West Germanic), Italic, Celtic))); c, conservative cognate coding with doubtful cognates excluded; d, all cognate sets with minimum topological constraints (Anatolian, Tocharian, (Greek, Armenian, Albanian, (Iranian, Indic), (Slavic, Baltic), (North Germanic, West Germanic), Italic, Celtic)); e, missing data coding with minimum topological constraints and all cognate sets. Shaded bars represent the implied age ranges under the two competing theories of Indo-European origin: blue, Kurgan hypothesis; green, Anatolian farming hypothesis. The relationship between the main language groups in the consensus tree for each analysis is also shown, along with posterior probability values.
High resolution image and legend (154K

One important advantage of the bayesian MCMC approach is that any inferences are not contingent on a specific tree topology. Trees are sampled in proportion to their posterior probability, providing a direct measure of uncertainty in the tree topology and branch-length estimates. By estimating divergence times across the MCMC sample distribution of trees, we can explicitly account for variability in the age estimates due to phylogenetic uncertainty, and hence calculate a confidence interval for the age of any node. We estimated divergence times by constraining the age of 14 nodes on each tree in accordance with historically attested events (see Supplementary Information). We then used penalized-likelihood rate smoothing to calculate divergence times without the assumption of rate constancy19. Another advantage of the bayesian framework is that prior knowledge of language relationships can be incorporated into the analysis. To ensure that the sample was consistent with well-established linguistic relationships, we filtered the 10,000-tree sample using a constraint tree (Fig. 1b). We used the resulting distribution of 3,500 estimates of basal divergence times to create a confidence interval for the age of the Indo-European language family (Fig. 1b).

A key part of any bayesian phylogenetic analysis is an assessment of the robustness of the inferences. One important potential cause of error is cognacy judgements. In the initial analysis, we included all cognate sets in the Dyen et al. database20 in an effort to maximize phylogenetic signal. To assess the impact of different levels of stringency in the cognacy judgements, we repeated the analysis after removing all cognate sets identified by Dyen et al. as 'doubtful'. 'Doubtful cognates' (for instance, possible chance similarities) could falsely increase similarities between languages and thus lead to an underestimate of the divergence times. Unrecognized borrowing between closely related languages would have a similar effect. Conversely, borrowing between distantly related languages will falsely inflate branch lengths at the base of the tree and thus increase divergence-time estimates. With the doubtful cognates removed, the conservative coding led to a similar estimate of Indo-European language relationships to that produced using the original coding. The relationships within each of the 11 main groups were unchanged. Only the placement of the weakly supported basal branches differed (Fig. 1c). More significantly, the divergence-time estimates increased, suggesting that the effects of chance similarities and unrecognized borrowings between closely related languages might have outweighed those of borrowings between distantly related languages. In other words, our initial analysis is likely to have underestimated the age of Indo-European.

The constraint tree used to filter the MCMC sample of trees also contained assumptions about Indo-European history that might have biased the results. We therefore repeated the analyses using a more relaxed set of constraints (Fig. 1d). This produced a divergence-time distribution and consensus tree almost identical to the original sample distribution (Fig. 1d).

Another potential bias lay in the initial coding procedure, which made no allowance for missing cognate information. The languages at the base of the tree (Hittite, Tocharian A and Tocharian B) may appear to lack cognates found in other languages because our knowledge of these extinct languages is limited to reconstructions from ancient texts. This uneven sampling might have increased basal branch lengths and thus inflated estimates of divergence times. We tested this possibility by recoding apparently absent cognates as uncertainties (absent or present) and re-running the analyses. Although divergence-time estimates decreased slightly, the effect was only small (Fig. 1e).

Finally, although there is considerable support for Hittite (an extinct Anatolian language) as the most appropriate root for Indo-European22, 23, rooting the tree with Hittite could be claimed to bias the analysis in favour of the Anatolian hypothesis. We thus re-ran the analysis using the consensus tree in Fig. 1 rooted with Balto-Slavic, Greek and Indo-Iranian as outgroups. This increased the estimated divergence time from 8,700 years bp to 9,600, 9,400 and 10,100 years bp, respectively.

Phylogenetic methods have revolutionized evolutionary biology over the past 20 years and are now starting to take hold in other areas of historical inference2, 23, 24, 27, 28, 29. The model-based bayesian framework used in this paper offers several advantages over previous applications of computational methods to language phylogenies. This approach allowed us to: identify sections in the language tree that were poorly supported; explicitly incorporate this uncertainty in tree typology and branch-length estimates in our analysis; test the possible effects of borrowing, chance similarities and bayesian priors on our analysis; and estimate divergence times without the assumption of a strict glottoclock. The challenge of making accurate inferences about human history is an extremely demanding one, requiring the integration of archaeological, genetic, cultural and linguistic data. The combination of computational phylogenetic methods and lexical data to test archaeological hypotheses is a step forward in this challenging and fascinating task.
Top of page
Methods
Data and coding

Data were sourced from the comparative Indo-European database created by Dyen et al.20. The database records word forms and cognacy judgements in 95 languages across the 200 items in the Swadesh word list. This list consists of items of basic vocabulary such as pronouns, numerals and body parts that are known to be relatively resistant to borrowing. For example, although English is a Germanic language, it has borrowed around 50% of its total lexicon from French and Latin. However, only about 5% of English entries in the Swadesh 200-word list are clear Romance language borrowings1. Where borrowings were obvious, Dyen et al. did not score them as cognate and thus they were excluded from our analysis; 11 of the speech varieties that were not coded by Dyen et al. were also excluded. To facilitate reconstruction of some of the oldest language relationships, we added three extinct Indo-European languages, thought to fit near the base of the tree (Hittite, Tocharian A and Tocharian B). Word form and cognacy judgements for all three languages were made on the basis of multiple sources to ensure reliability. The presence or absence of words from each cognate set was coded as '1' or '0', respectively, to produce a binary matrix of 2,449 cognates in 87 languages.
Tree construction

Language trees were constructed using a 'restriction site' model of evolution that allows unequal character-state frequencies and gamma-distributed character-specific rate heterogeneity (MrBayes version 2.01; ref. 30). We used default 'flat' priors for the rate matrix, branch lengths, gamma shape parameter and site-specific rates. The results were found to be robust to changes in these priors. For example, repeating the analyses with an exponential branch-length prior produced a 95% confidence interval for the basal divergence time of between 7,100 and 9,200 years BP.

The program was run ten times using four concurrent Markov chains. Each run generated 1,300,000 trees from a random starting phylogeny. On the basis of an autocorrelation analysis, only every 10,000th tree was sampled to ensure that consecutive samples were independent. A 'burn-in' period of 300,000 trees for each run was used to avoid sampling trees before the run had reached convergence. Log-likelihood plots and an examination of the post-burn-in tree topologies showed that the runs had indeed reached convergence by this time. For each analysis a total of 1,000 trees were sampled and rooted with Hittite. The branch between Hittite and the rest of the tree was split at the root such that half its length was assigned to the Hittite branch and half to the remainder of the tree; divergence-time estimates were found to be robust to threefold alterations of this allocation.
Divergence-time estimates

Eleven nodes corresponding to the points of initial divergence in all of the major language subfamilies were given minimum and/or maximum ages on the basis of known historical information (see Supplementary Information). The ages of all terminal nodes on the tree, representing languages spoken today, were set to zero by default. Hittite and the Tocharic languages were constrained in accordance with estimated ages of the source texts. Relatively broad date ranges were chosen to avoid making disputable, a priori assumptions about Indo-European history. A likelihood ratio test with the extinct languages removed revealed that rates were significantly non-clock-like (chi2 = 787.3, d.f. = 82, P < 0.001). Divergence-time estimates were thus made using the semi-parametric, penalized-likelihood model of rate variation implemented in R8s (version 1.50)19. The cross-validation procedure was applied to the majority-rule consensus tree (Fig. 1) to determine the optimal value of the rate-smoothing parameter. Step-by-step removal of each of the 14 age constraints on the consensus tree revealed that divergence-time estimates were robust to calibration errors. For 13 nodes, the reconstructed age was within 390 years of the original constraint range. Only the reconstructed age for Hittite showed an appreciable variation from the constraint range. This may be attributable to the effect of missing data associated with extinct languages. Reconstructed ages at the base of the tree ranged from 10,400 years bp with the removal of the Hittite age constraint, to 8,500 years bp with the removal of the Iranian group age constraint.

Pagel, M. in Time Depth in Historical Linguistics (eds Renfrew, C., McMahon, A. & Trask, L.) 189-207 (The McDonald Institute for Archaeological Research, Cambridge, UK, 2000)

Richards, M. et al. Tracing European founder lineage in the Near Eastern mtDNA pool. Am. J. Hum. Genet. 67, 1251-1276 (2000) | PubMed | ISI | ChemPort |

Chikhi, L., Nichols, R. A., Barbujani, G. & Beaumont, M. A. Y genetic data support the Neolithic Demic Diffusion Model. Proc. Natl Acad. Sci. USA 99, 11008-11013 (2002) | Article | PubMed | ChemPort |

Gimbutas, M. The beginning of the Bronze Age in Europe and the Indo-Europeans 3500-2500 B.C. J. Indo-Eur. Stud. 1, 163-214 (1973)

Mallory, J. P. Search of the Indo-Europeans: Languages, Archaeology and Myth (Thames & Hudson, London, 1989)

Renfrew, C. in Time Depth in Historical Linguistics (eds Renfrew, C., McMahon, A. & Trask, L.) 413-439 (The McDonald Institute for Archaeological Research, Cambridge, UK, 2000)

Swadesh, M. Lexico-statistic dating of prehistoric ethnic contacts. Proc. Am. Phil. Soc. 96, 453-463 (1952)

Bergsland, K. & Vogt, H. On the validity of glottochronology. Curr. Anthropol. 3, 115-153 (1962) | Article | ISI |

Blust, R. in Time Depth in Historical Linguistics (eds Renfrew, C., McMahon, A. & Trask, L.) 311-332 (The McDonald Institute for Archaeological Research, Cambridge, UK, 2000)

Steel, M. A., Hendy, M. D. & Penny, D. Loss of information in genetic distances. Nature 333, 494-495 (1988) | Article | PubMed | ChemPort |

Swofford, D. L., Olsen, G. J., Waddell, P. J. & Hillis, D. M. in Molecular Systematics (eds Hillis, D., Moritz, C. & Mable, B. K.) 407-514 (Sinauer Associates, Inc, Sunderland, Massachusetts, 1996)

Dixon, R. M. W. The Rise and Fall of Language (Cambridge Univ. Press, Cambridge, UK, 1997)

Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. Equations of state calculations by fast computing machines. J. Chem. Phys. 21, 1087-1091 (1953) | Article | ISI | ChemPort |

Sanderson, M. R8s, Analysis of Rates of Evolution,Version 1.50 (Univ. California, Davis, 2002)

Dyen, I., Kruskal, J. B. & Black, P. FILE IE-DATA1. Available at left fence[www.ntu.edu.au] fence (1997).

Sanderson, M. J. & Donoghue, M. J. Patterns of variation in levels of homoplasy. Evolution 43, 1781-1795 (1989) | ISI |

Gamkrelidze, T. V. & Ivanov, V. V. Trends in Linguistics 80: Indo-European and the Indo-Europeans (Mouton de Gruyter, Berlin, 1995)

Rexova, K., Frynta, D. & Zrzavy, J. Cladistic analysis of languages: Indo-European classification based on lexicostatistical data. Cladistics 19, 120-127 (2003) | Article | ISI |

Ringe, D., Warnow, T. & Taylor, A. IndoEuropean and computational cladistics. Trans. Philol. Soc. 100, 59-129 (2002) | Article | ISI |

Gkiasta, M., Russell, T., Shennan, S. & Steele, J. Neolithic transition in Europe: the radiocarbon record revisited. Antiquity 77, 45-62 (2003) | ISI |

Cavalli-Sforza, L. L., Menozzi, P. & Piazza, A. The History and Geography of Human Genes (Princeton Univ. Press, Princeton, 1994)

Holden, C. J. Bantu language trees reflect the spread of farming across sub-Saharan Africa: a maximum-parsimony analysis. Proc. R. Soc. Lond. B 269, 793-799 (2002) | Article | PubMed | ISI |

Barbrook, A. C., Howe, C. J., Blake, N. & Robinson, P. The phylogeny of The Canterbury Tales. Nature 394, 839 (1998) | Article | ISI | ChemPort |

McMahon, A. & McMahon, R. Finding families: Quantitative methods in language classification. Trans. Philol. Soc. 101, 7-55 (2003) | Article | ISI |

"Araştırmacılara göre Ötzi, Avrupalı çağdaşlarıyla karşılaştırıldığında, Anatolya'dan göç eden ilk çiftçilerle alışılmadık derecede yüksek bir genetik yüzdeye sahip." deniyor.
Ötzi'nin bilimsel anatomik tetkiki, bütün Avrupa medeniyeti'nin kaynağı olan yunanlıların atalarının da tıpkı Ötzi gibi tarihi Kürdistan coğrafyası'ndan gelip bugünkü Yunanistan'a yerleştikleri yönünde somut ve bilimsel bir kanıttır.

Eski yunanca incelendiğinde, eski kürdçe'ye tıpatıp benziyor. Dilbilimcilerin ileri sürdüğü ''Anatolya teorisi, Hint-Avrupa dillerinin tarım sanatının Anatolia'dan yaklaşık 8.000-9.500 yıl önce yayılmasıyla birlikte genişlediğini'' iddia ettiklerine göre, ve ayrıca yine dilbilimcilerin ve tarihçilerin araştırmalarına göre TARİM SANATINI İLK UYGULAYANLARIN Hint-Avrupa dilini geliştirdiklerine göre, o zaman Hint-Avrupa dilinin kökeni hiç şüphesiz: KÜRDÇE'dir.
Çünkü ilk tarım yapan kavim küdlerdir ve bu hem arkeolojij ve hemde tarih bilimi tarafından ispat edilmiş somut bir gerçektir.
Ötzi'nin 5300 yıllık bedeni, 1991 yılında italyan Alplerindeki bir buzulda keşfedildi

Avrupalı araştırmacılar: Buzadam Ötzi, Anadolu'dan geldi; koyu tenli ve keldi

Yayınlandı 16/08/2023

Mevcut bilgilere göre boyu 1.60 metrenin biraz altında olan Ötzi, yaklaşık 50 kg ağırlığındaydı ve bir okla öldürülmüştü.

Almanya'da Max Planck Antropoloji Enstitüsü'nün yaptığı araştırmaya göre Avrupa'nın en ünlü mumyası buzadam Ötzi'nin ataları Anadolu'dan geldi.

İtalya'daki Eurac Mumya Araştırma Enstitüsü ile işbirliği içinde yürütülen yeni çalışmada, ünlü mumyanın genom analizleri yapıldı.

Araştırma sonuçlarına göre beş bin yaşından büyük olan Ötzi sanılanın aksine daha koyu bir tene sahipti. Ötzi'nin ayrıca 'kel olduğu' sonucuna varıldı.

Eurac Enstitüsü'nden raporun eş yazarı Albert Zink, analizleri yapılan genlerinin kelliğe yatkınlık gösterdiğini ve bunun da "yaşı 45 civarında olan mumyada neredeyse hiç saç bulunmadığı" sonucunu ortaya çıkardığını belirtiyor.

Bilim insanlarının yeni araştırmalarına göre on yıllar önce İtalyan Alplerinde bulunan buzadam Ötzi, günümüz Anadolu topraklarından geliyorduSouth Tyrol Museum of Archaeology/Ochsenreiter

Araştırmacılar, 2012'de çözülen genom şifresini gelişmiş dizileme yöntemleriyle daha da ileri boyuta taşımıştı. Araştırmacılara göre Ötzi, Avrupalı çağdaşlarıyla karşılaştırıldığında, Anadolu'dan göç eden ilk çiftçilerle alışılmadık derecede yüksek bir genetik yüzdeye sahip.

Çalışmada mumyanın derisinin, sanılanın aksine, buzda kaldığı için koyulaşmadığını da gören araştırmacılar, bunun "Ötzi'nin orijinal ten rengi" olmasının muhtemel olduğunu kaydetti.

"Anadolu'dan geldi"

Max Planck'ta araştırmacı olan ve çalışmanın eş yazarı Johannes Krause, "Ötzi'nin yeni genomunda Doğu Avrupalı bozkır çobanlarından hiçbir iz bulamamak bizi çok şaşırttı ve avcı-toplayıcı genlerin oranı da çok düşük" diyor.

Krause, "Genetik olarak, atalarının doğrudan Anadolu'dan geldiği görülüyor" diye ekliyor.

Ötzi 1991 yılında İtalyan Alplerindeki bir buzulda keşfedildi.

O zamandan beri bilim insanları, en modern teknikleri kullanarak, keşfi büyük yankı yaratan Ötzi'nin hayat izini sürmeye devam ediyor.

Mevcut bilgilere göre boyu 1.60 metrenin biraz altında olan Ötzi, yaklaşık 50 kg ağırlığındaydı ve bir okla öldürülmüştü.

Çalışmalara göre Ötzi'nin ölmeden önceki son yemeği büyük olasılıkla kurutulmuş dağ keçisi etiydi.

Mumya, Bolzano'daki Alto Adige Arkeoloji Müzesi'nde soğuk bir odada muhafaza ediliyor.

(EuroNews)

Historiska Kurdistan -
Civilisationens Grogrund

HISTORICAL RUINS OF KURDISTAN

İLKLERİN YURDU

ZIMANÊ KURDÎ (Kurdish)

LÊKOLÎN

Foundation For Kurdish Library & Museum